Die Efronwürfel
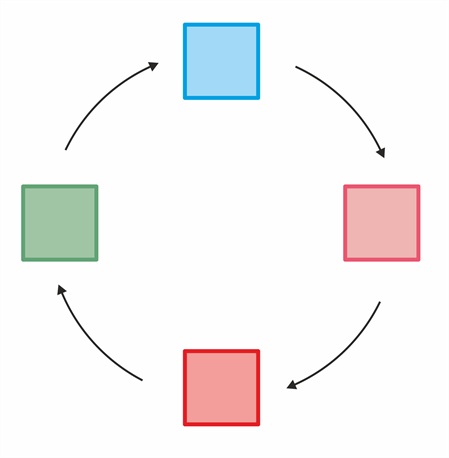
Die Efronwürfel demonstrieren eine sogenannte intransitive Relation.
Viele Zusammenhänge in unserem Leben sind transitiv:
Wenn Mathelde älter ist als Minus und Norman älter ist als Mathelde,
dann ist Norman auch älter als Minus.
Wären Efrons Würfel auch transitiv, würde ein Würfel immer gegen die drei anderen gewinnen.
Tatsächlich ist es aber so, dass der blaue Würfel den rosanen in zwei Drittel aller Fälle schlägt, das Gleiche gilt für den rosanen
gegen den roten Würfel. Rot schlägt wiederum grün und grün den blauen Würfel. Es ist also egal welchen Würfel wir wählen, der Spieler, der als zweites wählt, wird immer einen Würfel finden, der in mehr als der Hälfte aller Fälle gewinnt.
Ein weiteres Beispiel für eine intransitive Relation ist das Spiel "Schere, Stein, Papier", bei dem jedes Symbol gegen eines gewinnt und gegen ein anderes verliert.
Auch aus dem Sport kennen wir intransitive Relationen. Wenn Deutschland in der nächsten WM gegen Frankreich gewinnt und England gegen Deutschland, gewinnt England nicht automatisch gegen Frankreich. Oder?
Bei Transitivität ist A besser als B und B besser als C.
Somit ist A automatisch besser als C.
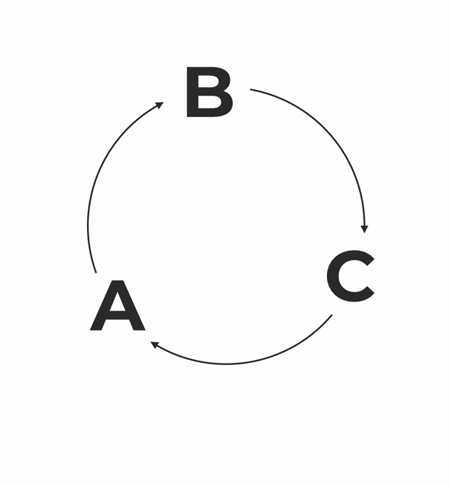
Bei Intransitivität ist A besser als B und B besser als C.
Allerdings ist in diesem Fall C besser als A. Es schließt sich also ein Kreis.
Wenn drei Würfel im Spiel sind ändert sich alles.
Der letzte Spieler verliert seinen Vorteil.
Für den ersten Spieler gibt es auf den ersten Blick zwei "beste Würfel": rosa und rot.
Dies zeigt ein Blick auf die Wahrscheinlichkeitsverteilung in allen möglichen Würfelkombinationen (Werte gerundet).
Rot und Rosa sind zweimal der beste, aber nie der schlechteste Würfel.
Setzt man voraus, dass alle Spieler diese Wahrscheinlichkeitsverteilung kennen und ihren Würfel optimal auswählen, ergibt sich jedoch ein anderes Bild.
Fall 1:
Der erste Spieler wählt den roten Würfel.
Dann wählt der zweite Spieler den rosa Würfel, da grün immer schlechter ist als rot und blau höchstens einen Gleichstand erreichen kann.
Der dritte Spieler wählt folglich blau, womit die Siegchancen für alle Spieler am Ende gleich sind.
Fall 2:
Der erste Spieler wählt den rosa Würfel.
Dann wählt der zweite Spieler den blauen Würfel, da grün immer schlechter ist als rosa und rot höchstens einen Gleichstand erreichen kann.
Der dritte Spieler wählt folglich blau, womit auch hier die Siegchancen für alle Spieler am Ende gleich sind.
Fall 3:
Der erste Spieler wählt den blauen Würfel.
Dann wählt der zweite Spieler den roten Würfel, da rosa im besten Falle einen Gleichstand erzielt. Die Wahl von grün würde automatisch dazu führen, dass der dritte Spieler mit der Wahl des roten Würfels am wahrscheinlichsten gewinnt.
Der dritte Spiele wählt folglich rosa, womit die Siegchancen erneut für alle Spieler gleich sind.
Fall 4:
Kein Spieler würde als erstes den grünen Würfel wählen, womit dieser Fall hinfällig ist.
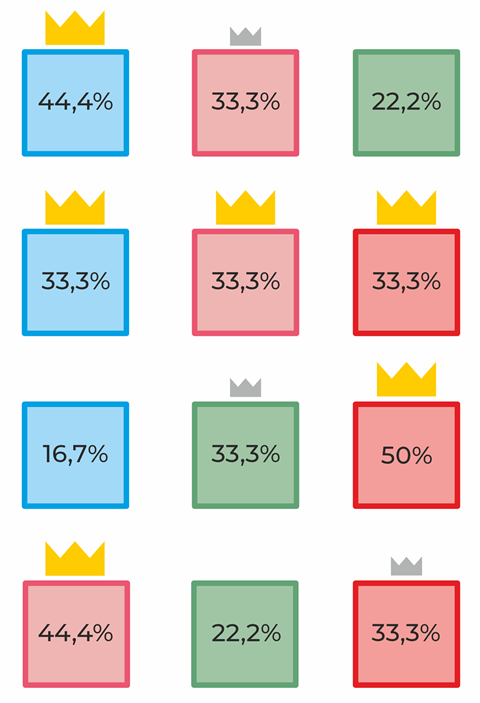
Sind alle vier Würfel im Spiel, ergibt sich im Übrigen folgende Wahrscheinlichkeitsverteilung:
ICH MACH MATHE!
im Z²
Große Langgasse 8
55116 Mainz
Eingang:
Gymnasiumstraße
+49 6131 - 49 89 352
ÖFFNUNGSZEITEN
Wir haben leider nicht jeden Tag geöffnet. Unsere Ausstellungstage findest Du hier.
EINTRITTSPREISE
9,50 € / ermäßigt 6,50 € / Familie 27,00 €
"Ich mach Mathe!" ist eine
Mitmachausstellung der
Z Quadrat GmbH